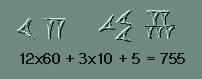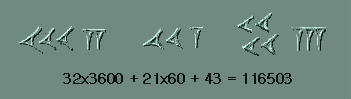|
Mucho más efectivos que los sitemas anteriores
son los posicionales. En ellos la posición de una cifra nos dice
si son decenas, centenas ... o en general la potencia de la base correspondiente.
Sólo tres culturas además de la india lograron desarrollar
un sistema de este tipo. Babilonios, chinos y mayas en distintas épocas
llegaron al mismo principio. La ausencia del cero impidió a los
chinos un desarrollo completo hasta la intraducción del mismo.
Los sistemas babilónico y maya no eran prácticos para
operar porque no disponían de simbolos particulares para los
dígitos, usando para representarlos una acumulación del
signo de la unidad y la decena. El hecho que sus bases fuese 60 y 20
respectivamente no hubiese representado en principio nigún obstáculo.
Los mayas por su parte cometían una irregularidad a partir de
las unidades de tercer orden, ya que detrás de las veintenas
no usaban 20x20=400 sino 20x18=360 para adecuar los números al
calendario, una de sus mayores preocupaciones culturales.
Fueron los indios antes del siglo VII los que idearon el sistema tal
y como hoy lo conocemos, sin más que un cambio en la forma en
la que escribimos los nueve dígitos y el cero. Aunque con frecuencia
nos referimos a nuestro sistema de numeración cómo árabe,
las pruebas arqueológicas y documentales demuestran el uso del
cero (tanto en posiciones intermedias como finales) en la India anteriormente.
Los árabes transmitieron esta forma de representar los números
y sobre todo el cáculo asociado a ellas, aunque tardaron siglos
en ser usadas y aceptadas. Una vez más se produjo una gran resistencia
a algo por el mero hecho de ser nuevo o ajeno, aunque sus ventajas eran
evidentes. Sin esta forma eficaz de numerar y efectuar cálculos
dificilmente la ciencia hubiese podido avanzar.
SISTEMA NUMÉRICO BABILÓNICO
Entre la muchas civilizaciones que florecieron en la antigua Mesopotamia
se desarrollaron distintos sistemas de numeración. El más
representativo de ellos fue un sistema de base 10, aditivo hasta el
60 y posicional para números superiores. Para la unidad se usaba
la marca vertical que se hacía con el punzón en forma
de cuña. Se ponían tantas marcas como fuera preciso hasta
llegar a 10, que tenía su propio signo.

De este se usaban los que fuera necesario
completando con las unidades hasta llegar a 60.

A partir de ahí se usaba un sistema posicional
en el que los grupos de signos iban representando sucesivamente el número
de unidades, 60, 60x60, 60x60x60 y asi sucesivamente como en los ejemplos
que se acompañan.

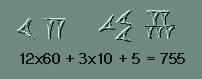 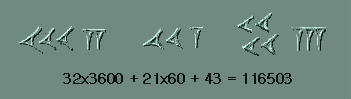
SISTEMA DE NUMERACIÓN MAYA
Los mayas idearon un sistema de base 20 con el 5 cómo base auxiliar.
La unidad se representaba por un punto. Dos, tres, y cuatro puntos servían
para 2, 3 y 4. El 5 era una raya horizontal, a la que se añadían
los puntos necesarios para representar 6, 7, 8 y 9. Para el 10 se usaban
dos rayas, y de la misma forma se continúa hasta el 20, con cuatro
rayas.
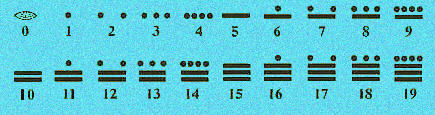
Hasta aquí parece ser un sistema de base 5 aditivo,
pero en realidad, considerados cada uno un solo signo, estos símbolos
constituyen las cífras de un sistema de base 20, en el que hay
que multiplicar el valor de cada cifra por 1, 20, 20x20, 20x20x20 ...
según el lugar que ocupe, y sumar el resultado. Es por tanto
un sistema posicional que se escribe a arriba abajo, empezando por el
orden de magnitud mayor.
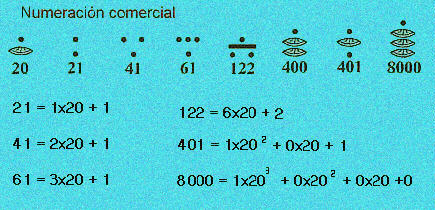
Al tener cada cifra un valor relativo según el lugar que ocupa,
la presencia de un signo para el cero, con el que indicar la ausencia
de unidades de algún orden, se hace imprescindible y los mayas
lo usaron, aunque no parece haberles interesado el concepto de cantidad
nula. Cómo los babilonios lo usaron simplemente para indicar
la ausencia de otro número.
Pero los científicos mayas eran a la vez sacerdotes ocupados
en la observación astronómica y para expresar los número
correspondientes a las fechas usaron unas unidades de tercer orden irregulares
para la base 20. Así la cifra que ocupaba el tercer lugar desde
abajo se multiplicaba por 20x18=360 para completar una cifra muy próxima
a la duración de un año.

El año lo consideraban dividido en 18 uinal que constaba cada
uno de 20 días. Se añadían algunos festivos (uayeb)
y de esta forma se conseguía que durara justo lo que una de las
unidades de tercer orden del sistema numérico. Además
de éste calendario solar, usaron otro de carater religioso en
el que el año se divide en 20 ciclos de 13 días.
Al romperse la unidad del sistema éste se hace poco práctico
para el cálculo y aunque los conocimiento astronómicos
y de otro tipo fueron notables, los mayas no desarrollaron una matemática
más allá del calendario.
|